The Web Site of L.A.P.

Roulette Curves with Gnu/Linux

1) A Very Complex Roulette: Ellipse Rolling on Ellipse

We now consider an ellipse rolling on another ellipse. I am intrigued by such curves owing to their mathematical complexity rather than any stunning visual appearance. Again, the reader is encouraged to become familiar with the basic method of roulette generation as outlined in the introductory article.

First, we define the fixed curve, which is an ellipse in standard form centered at the origin of the complex plane, and its derivative. The variables af, bf denote those of the fixed curve, while the rolling is defined using ar, br.

The rolling curve, sitting atop the fixed ellipse, must properly map onto the fixed ellipse. This necessitates for the fixed ellipse a clockwise rotation beginning at the point 0, i * b:
(%i2) kill ( all ) $
define ( fx ( t , af , bf ) , trigsimp ( af · cos ( − t + %pi / 2 ) + %i · bf · sin ( − t + %pi / 2 ) ) ) ;
define ( dfx ( t , af , bf ) , diff ( fx ( t , af , bf ) , t ) ) ;

\[\operatorname{ }\operatorname{fx}\left( t\operatorname{,}\ensuremath{\mathrm{af}}\operatorname{,}\ensuremath{\mathrm{bf}}\right) \operatorname{:=}\ensuremath{\mathrm{af}} \sin{(t)}+i \ensuremath{\mathrm{bf}} \cos{(t)}\]

\[\operatorname{ }\operatorname{dfx}\left( t\operatorname{,}\ensuremath{\mathrm{af}}\operatorname{,}\ensuremath{\mathrm{bf}}\right) \operatorname{:=}\ensuremath{\mathrm{af}} \cos{(t)}-i \ensuremath{\mathrm{bf}} \sin{(t)}\]

The arc length of the fixed ellipse, since it involves elliptic integrals, can't be determined by Maxima, but from other sources (e.g. Wolfram Alpha) we determine it as:
(%i3) sfx ( t , af , bf ) : = af · elliptic_e ( t , 1 − bf ^ 2 / af ^ 2 ) ;

\[\operatorname{ }\operatorname{sfx}\left( t\operatorname{,}\ensuremath{\mathrm{af}}\operatorname{,}\ensuremath{\mathrm{bf}}\right) \operatorname{:=}\ensuremath{\mathrm{af}} \operatorname{elliptic\_ e}\left( t\operatorname{,}1-\frac{{{\ensuremath{\mathrm{bf}}}^{2}}}{{{\ensuremath{\mathrm{af}}}^{2}}}\right) \]

Now come the defining equations for the rolling ellipse, which sits atop the fixed curve at the point 0, i * b. We use the accessory variable cr to define an upward displacement.
(%i6) define ( ro ( u , ar , br , cr ) , trigexpand ( trigsimp ( ar · cos ( u − %pi / 2 ) + %i · br · sin ( u − %pi / 2 ) ) ) + %i · cr ) ;
define ( dro ( u , ar , br ) , diff ( ro ( u , ar , br , cr ) , u ) ) ;
sro ( u , ar , br ) : = ar · elliptic_e ( u , 1 − br ^ 2 / ar ^ 2 ) ;

\[\operatorname{ }\operatorname{ro}\left( u\operatorname{,}\ensuremath{\mathrm{ar}}\operatorname{,}\ensuremath{\mathrm{br}}\operatorname{,}\ensuremath{\mathrm{cr}}\right) \operatorname{:=}\ensuremath{\mathrm{ar}} \sin{(u)}-i \ensuremath{\mathrm{br}} \cos{(u)}+i \ensuremath{\mathrm{cr}}\]

\[\operatorname{ }\operatorname{dro}\left( u\operatorname{,}\ensuremath{\mathrm{ar}}\operatorname{,}\ensuremath{\mathrm{br}}\right) \operatorname{:=}i \ensuremath{\mathrm{br}} \sin{(u)}+\ensuremath{\mathrm{ar}} \cos{(u)}\]

\[\operatorname{ }\operatorname{sro}\left( u\operatorname{,}\ensuremath{\mathrm{ar}}\operatorname{,}\ensuremath{\mathrm{br}}\right) \operatorname{:=}\ensuremath{\mathrm{ar}} \operatorname{elliptic\_ e}\left( u\operatorname{,}1-\frac{{{\ensuremath{\mathrm{br}}}^{2}}}{{{\ensuremath{\mathrm{ar}}}^{2}}}\right) \]

Let's plot the initial condition based on these definitions:
(%i8) load ( draw ) $
set_draw_defaults ( xrange = [ − 4 , 4 ] , yrange = [ − 4 , 4 ] , proportional_axes = xy , nticks = 200 ,
grid = true , background_color = light_yellow , xlabel = "Real Axis" , ylabel = "Imaginary Axis" ) $
(%i14) ar : 1 / 4 $ br : 1 / 2 $
af : 2 $ bf : 1 $
cr : bf + br $
wxdraw2d ( color = blue , parametric ( realpart ( ro ( u , ar , br , cr ) ) , imagpart ( ro ( u , ar , br , cr ) ) , u , 0 , 2 · %pi ) ,
color = red , parametric ( realpart ( fx ( t , af , bf ) ) , imagpart ( fx ( t , af , bf ) ) , t , 0 , 2 · %pi ) ,
   title = "Ellipse on Ellipse Initial Condition"
   ) $

\[\operatorname{ }\]

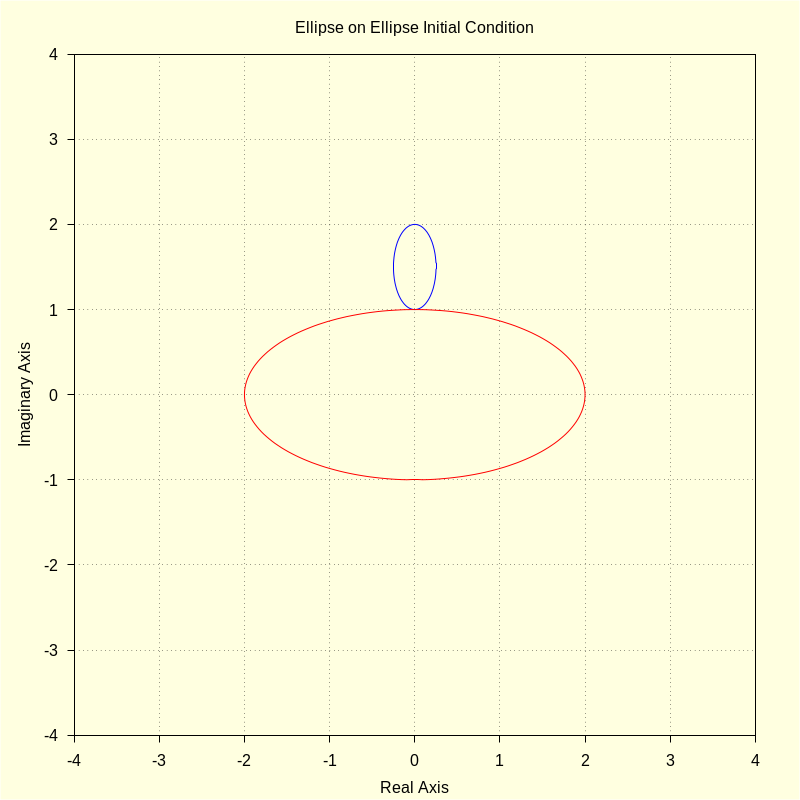
(Graphics)
To insure a no-slip roll, we must get u = f(t).
We equate arc lengths: af*elliptic_e(t,1-bf^2/af^2) = ar*elliptic_e(u,1-br^2/ar^2).
The inversion of an elliptic integral of the second kind is not possible (aside from very complex extraordinary methods) and hence we invert the function numerically.
(%i15) load ( newton1 ) $
As a check, we pick an arbitrary value for t, find the numerical root, u(t), and then substitute back into the rolling curve arc length to see if it equals the fixed curve arc length.
(%i22) kill ( t , u ) $
ar : 1 / 4 $ br : 1 / 2 $ af : 2 $ bf : 1 $
t : 4 . 0 ;
ut : newton ( sro ( u , ar , br ) − sfx ( t , af , bf ) , u , t , 1e-10 ) ;

\[\operatorname{(t) }4.0\]

\[\operatorname{(ut) }16.76796630164899\]

Are the two arc lengths equal?
(%i24) sfx ( t , af , bf ) ;
sro ( ut , ar , br ) ;

\[\operatorname{ }6.413548139974258\]

\[\operatorname{ }6.413548139993162\]

OK. To many decimal places they are equal.
Now, as in the example of the ellipse rolling on the line, we determine the factor, du/dt, to be able to find the derivative of the rolling curve at each step of t during the roulette generation.
(%i27) kill ( t , u , af , bf , ar , br ) $
depends ( u , t ) $
define ( dudt ( t , u , af , bf , ar , br ) , rhs ( solve ( factor ( cabs ( diff ( ro ( u , ar , br , cr ) , t ) ) ) = cabs ( dfx ( t , af , bf ) ) , diff ( u , t ) ) [ 1 ] ) ) ;

\[\operatorname{ }\operatorname{dudt}\left( t\operatorname{,}u\operatorname{,}\ensuremath{\mathrm{af}}\operatorname{,}\ensuremath{\mathrm{bf}}\operatorname{,}\ensuremath{\mathrm{ar}}\operatorname{,}\ensuremath{\mathrm{br}}\right) \operatorname{:=}\frac{\sqrt{{{\ensuremath{\mathrm{bf}}}^{2}} {{\sin{(t)}}^{2}}+{{\ensuremath{\mathrm{af}}}^{2}} {{\cos{(t)}}^{2}}}}{\sqrt{{{\ensuremath{\mathrm{br}}}^{2}} {{\sin{(u)}}^{2}}+{{\ensuremath{\mathrm{ar}}}^{2}} {{\cos{(u)}}^{2}}}}\]

2) Generate the Roulette

Everything is adequately defined and we now produce some rouletes.

For the first example, we select p, the generating point, to be at the center of the rolling ellipse.
(%i28) M : zeromatrix ( 600 , 2 ) $
(%i34) kill ( t , u , af , bf , ar , br ) $
ar : 1 / 4 $ br : 1 / 2 $ af : 2 $ bf : 1 $
p : %i · ( bf + br ) ;

\[\operatorname{(p) }\frac{3 i}{2}\]

(%i37) t : 0 $ tinc : 0 . 015 $
for i : 1 thru 600 step 1 do (
u : newton ( sro ( uu , ar , br ) − sfx ( t , af , bf ) , uu , t , 1e-10 ) ,
roul : fx ( t , af , bf ) − ( ro ( u , ar , br , ( br + bf ) ) − p ) · dfx ( t , af , bf ) / ( dro ( u , ar , br ) · dudt ( t , u , af , bf , ar , br ) ) ,
M [ i , 1 ] : float ( realpart ( roul ) ) ,
M [ i , 2 ] : float ( imagpart ( roul ) ) ,
t : t + tinc
) $
(%i40) kill ( u , t ) $
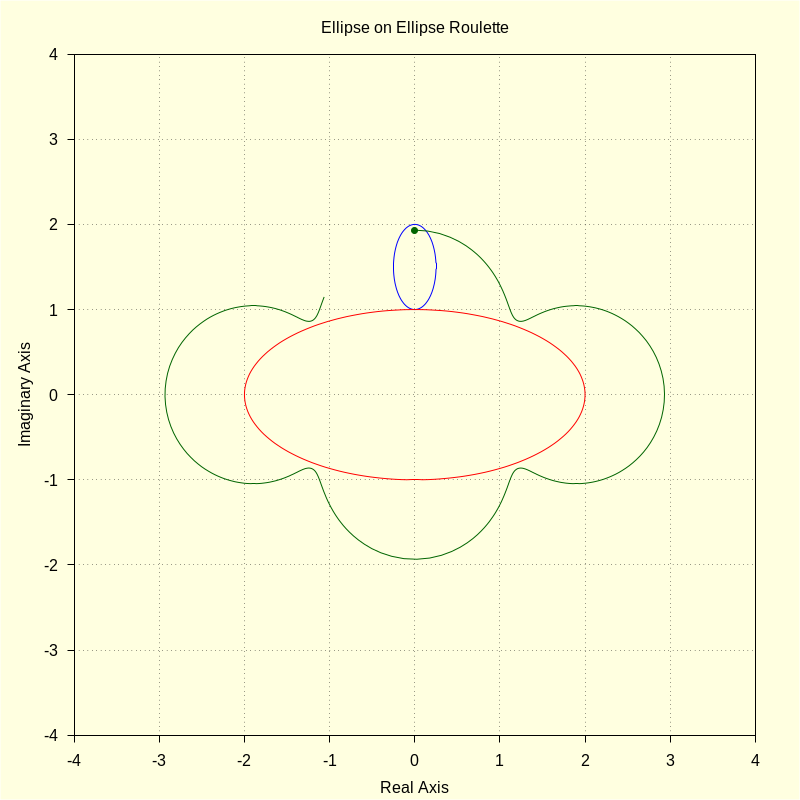
wxdraw2d ( color = blue , parametric ( realpart ( ro ( u , ar , br , ( br + bf ) ) ) , imagpart ( ro ( u , ar , br , ( br + bf ) ) ) , u , 0 , 2 · %pi ) ,
   color = red , parametric ( realpart ( fx ( t , af , bf ) ) , imagpart ( fx ( t , af , bf ) ) , t , 0 , 2 · %pi ) ,
   color = darkgreen , point_size = 1 , point_type = 7 , points ( [ [ realpart ( p ) , imagpart ( p ) ] ] ) , point_type = 0 , points_joined = true , points ( M ) ,
   title = "Ellipse on Ellipse Roulette"
) $

\[\operatorname{ }\]

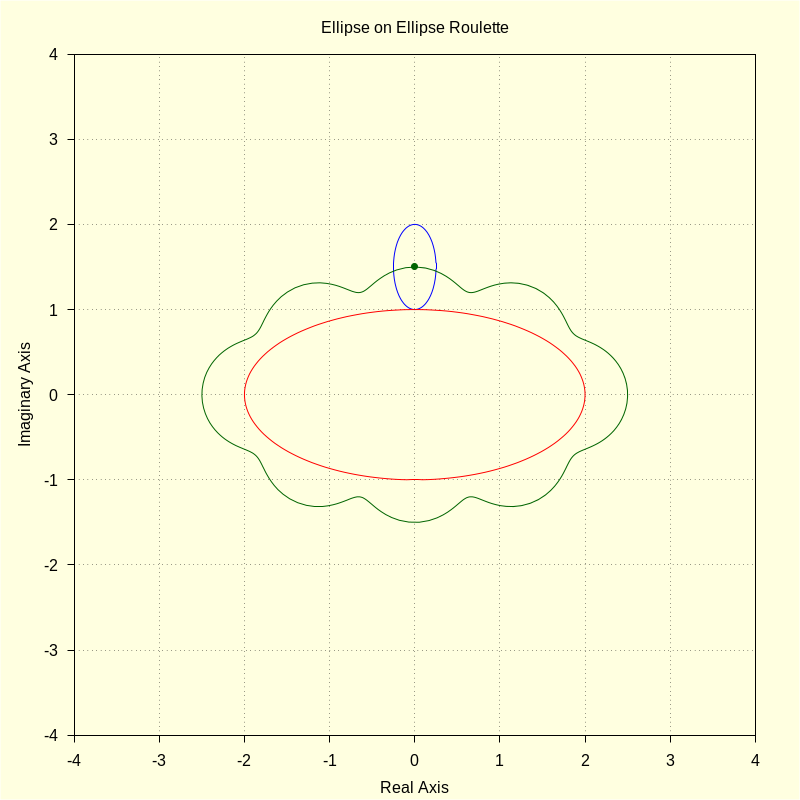
(Graphics)
In this case, the parameters of the two ellipses are proportional and thus the roulette will close after each revolution (or after an integral number of revolutions).

The next example shows an incommensurate case.
(%i46) kill ( t , u , af , bf , ar , br ) $
ar : 1 / 5 $ br : 1 / sqrt ( 10 ) $ af : 2 $ bf : 1 $
p : %i · ( bf + br ) ;

\[\operatorname{(p) }\left( \frac{1}{\sqrt{10}}+1\right) i\]

(%i49) t : 0 $ tinc : 0 . 02 $
for i : 1 thru 600 step 1 do (
u : newton ( sro ( uu , ar , br ) − sfx ( t , af , bf ) , uu , t , 1e-10 ) ,
roul : fx ( t , af , bf ) − ( ro ( u , ar , br , ( br + bf ) ) − p ) · dfx ( t , af , bf ) / ( dro ( u , ar , br ) · dudt ( t , u , af , bf , ar , br ) ) ,
M [ i , 1 ] : float ( realpart ( roul ) ) ,
M [ i , 2 ] : float ( imagpart ( roul ) ) ,
t : t + tinc
) $
(%i52) kill ( u , t ) $
wxdraw2d ( color = blue , parametric ( realpart ( ro ( u , ar , br , ( br + bf ) ) ) , imagpart ( ro ( u , ar , br , ( br + bf ) ) ) , u , 0 , 2 · %pi ) ,
   color = red , parametric ( realpart ( fx ( t , af , bf ) ) , imagpart ( fx ( t , af , bf ) ) , t , 0 , 2 · %pi ) ,
   color = darkgreen , point_size = 1 , point_type = 7 , points ( [ [ realpart ( p ) , imagpart ( p ) ] ] ) , point_type = 0 , points_joined = true , points ( M ) ,
   title = "Ellipse on Ellipse Roulette"
) $

\[\operatorname{ }\]

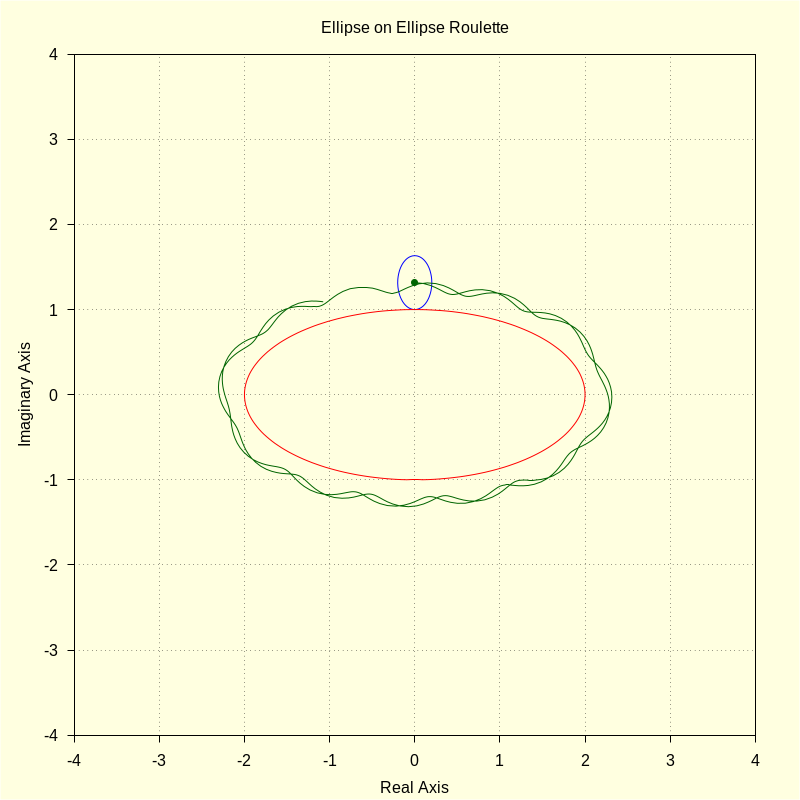
(Graphics)
We now place p beyond the top of the rolling ellipse.
(%i58) kill ( t , u , af , bf , ar , br ) $
ar : 1 / 4 $ br : 1 / 2 $ af : 2 $ bf : 1 $
p : %i · ( bf + br + 1 ) ;

\[\operatorname{(p) }\frac{5 i}{2}\]

(%i61) t : 0 $ tinc : 0 . 01 $
for i : 1 thru 600 step 1 do (
u : newton ( sro ( uu , ar , br ) − sfx ( t , af , bf ) , uu , t , 1e-10 ) ,
roul : fx ( t , af , bf ) − ( ro ( u , ar , br , ( br + bf ) ) − p ) · dfx ( t , af , bf ) / ( dro ( u , ar , br ) · dudt ( t , u , af , bf , ar , br ) ) ,
M [ i , 1 ] : float ( realpart ( roul ) ) ,
M [ i , 2 ] : float ( imagpart ( roul ) ) ,
t : t + tinc
) $
(%i64) kill ( u , t ) $
wxdraw2d ( color = blue , parametric ( realpart ( ro ( u , ar , br , ( br + bf ) ) ) , imagpart ( ro ( u , ar , br , ( br + bf ) ) ) , u , 0 , 2 · %pi ) ,
   color = red , parametric ( realpart ( fx ( t , af , bf ) ) , imagpart ( fx ( t , af , bf ) ) , t , 0 , 2 · %pi ) ,
   color = darkgreen , point_size = 1 , point_type = 7 , points ( [ [ realpart ( p ) , imagpart ( p ) ] ] ) , point_type = 0 , points_joined = true , points ( M ) ,
   title = "Ellipse on Ellipse Roulette"
) $

\[\operatorname{ }\]

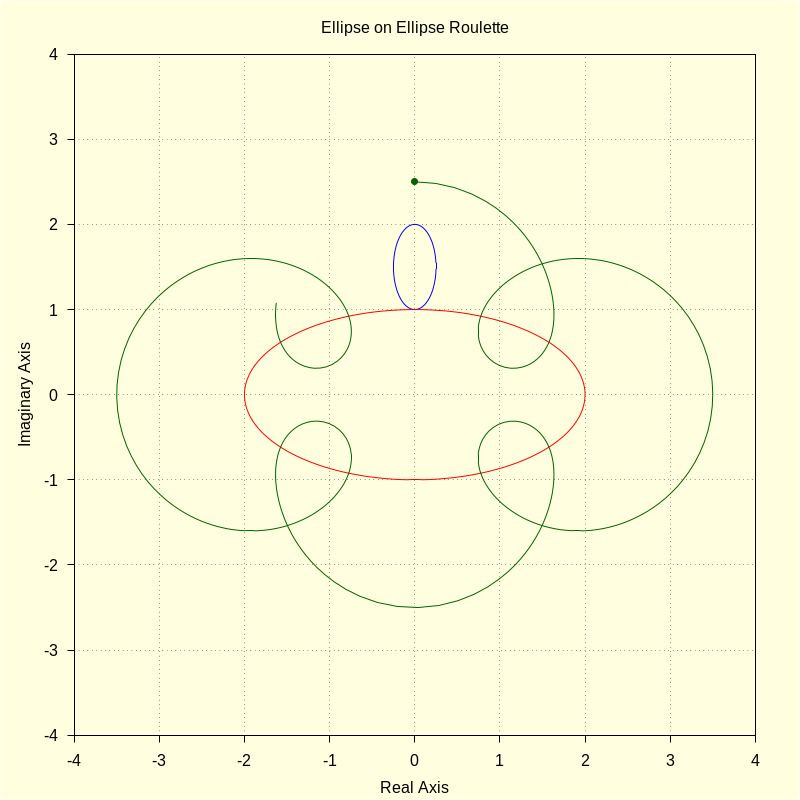
(Graphics)
Finally, we locate p at the upper focus of the rolling ellipse.
(%i70) kill ( t , u , af , bf , ar , br ) $
ar : 1 / 4 $ br : 1 / 2 $ af : 2 $ bf : 1 $
p : %i · ( bf + br + sqrt ( br ^ 2 − ar ^ 2 ) ) ;

\[\operatorname{(p) }\left( \frac{\sqrt{3}}{4}+\frac{3}{2}\right) i\]

(%i73) t : 0 $ tinc : 0 . 01 $
for i : 1 thru 600 step 1 do (
u : newton ( sro ( uu , ar , br ) − sfx ( t , af , bf ) , uu , t , 1e-10 ) ,
roul : fx ( t , af , bf ) − ( ro ( u , ar , br , ( br + bf ) ) − p ) · dfx ( t , af , bf ) / ( dro ( u , ar , br ) · dudt ( t , u , af , bf , ar , br ) ) ,
M [ i , 1 ] : float ( realpart ( roul ) ) ,
M [ i , 2 ] : float ( imagpart ( roul ) ) ,
t : t + tinc
) $
(%i76) kill ( u , t ) $
wxdraw2d ( color = blue , parametric ( realpart ( ro ( u , ar , br , ( br + bf ) ) ) , imagpart ( ro ( u , ar , br , ( br + bf ) ) ) , u , 0 , 2 · %pi ) ,
   color = red , parametric ( realpart ( fx ( t , af , bf ) ) , imagpart ( fx ( t , af , bf ) ) , t , 0 , 2 · %pi ) ,
   color = darkgreen , point_size = 1 , point_type = 7 , points ( [ [ realpart ( p ) , imagpart ( p ) ] ] ) , point_type = 0 , points_joined = true , points ( M ) ,
   title = "Ellipse on Ellipse Roulette"
) $

\[\operatorname{ }\]

(Graphics)

3) Epilogue

As already stated, the primary allure, to me, of these roulettes is not the aesthetics of the patterns but rather it is the mathematical complexity of the derivations. Conic sections, like the ellipse or parabola, are intuitively very simple curves. The mind can comprehend them with ease. But to describe their properties mathematically is a far more difficult undertaking.

Created with wxMaxima.
Modified and embedded by L.A.P.